Inverse filtering

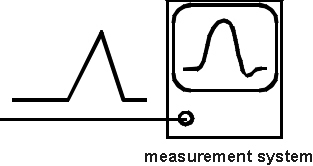
Our aim is to measure broad band time or other domain waveforms. If the bandwidth of the signal to be measured is larger than that of the measurement system the recorded waveform will be a distorted version of the original one. Assuming that the distortion is known the measurement can be partly compensated for it. This process is called inverse filtering.

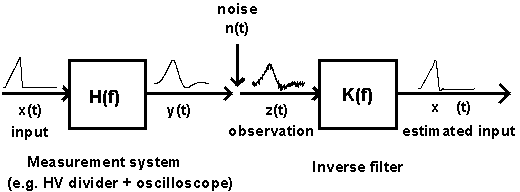
The main problem of the inverse filtering process is that measurement noise (quantization noise, electromagnetic interference etc.) is amplified in a great extent, hiding many times the useful signal completely. This noise has to be suppressed on the price of bias in the reconstructed signal. A good compromise has to be found between the noisy and biased reconstruction. The inverse filtering process should be adaptive to the signal to be measured and to the noise.

Applications:

• reconstruction of out-of-focus images,
• improvement of high voltage lightning impulse measurements ,
• improvement of the bandwidth of high-speed sampling oscilloscopes,
• spectroscopy,
• inverse filtering of room acoustics,

• "Cyber-Physical Systems" European Union, European Social Fund (TÁMOP-4.2.2.C-11/1/KONV-2012-0001), 2012-2014, 3 years. Principal investigator: T. Dabóczi
• "Parameter Estimation and Modelling, Based on Signal Processing" Hungarian Scientific Research Fund, 2008-2011, 3 years. Principal investigator: I. Kollar
• "Model Based Digital Signal Processing" Hungarian Scientific Research Fund, 2005-2008, 3 years. Principal investigator: I. Kollar
• "Global optimization of inverse filtering and identification" Hungarian Scientific Research Fund, 2001-2003, 3 years. Principal investigator: T. Dabóczi.
• "Inverse filtering and its applications " (Ref. No: OTKA F026136) Hungarian Scientific Research Fund, 1998-2000, 3 years. Principal investigator: T. Dabóczi.
• "Deconvolution of Fast Electrical Pulses for Standard Purposes " (Ref. No: 43NANB614883)  National Institute of Standards and Technology (NIST), USA, 1996-97, 1 year. Principal investigator: T. Dabóczi.
• "Intelligent deconvolution system" (Ref. No: OTKA F016457) Hungarian Scientific Research Fund, 1995-1997, 3 years. Principal investigator: T. Dabóczi.
• "Investigation, development and application of deconvolution algorithms" (Ref. No.:OTKA780) Hungarian Scientific Research Fund, 1991-1994, 4 years. Principal investigator: I. Kollár.

Contact person:

Tamás Dabóczi, PhD
Dept. of Measurement and Information Systems
Budapest University of Technology and Economics
H-1521 Budapest, Hungary

Phone:    +36 1 463-2065
Fax:        +36 1 463-4112
Url:        http://www.mit.bme.hu/~daboczi/
Email:    daboczi@mit.bme.hu