Transfer function modeling and equalization by fixed-pole parallel filters

This page contains a short description, list of related publications (all downloadable as pdf), and MATLAB code for fixed-pole parallel filter design. The description is intended to give a broader view about the parallel filter and a starting point to my related publications. (Note that this page does not contain references to other related work, like warped or Kautz filters. The references can be found in my publications available in pdf).

Jump to a tutorial video and slides

Jump to the publications about the parallel filter

Jump to the MATLAB and Octave code

1 Introduction

The problem of modeling or equalizing a given transfer function by a digital filter comes up frequently in the field of digital signal processing. As opposed to the linear frequency resolution of traditional FIR and IIR design algorithms, some tasks require more flexible allocation of frequency resolution. For example, in audio applications logarithmic frequency resolution is desirable, since that corresponds to the resolution of human hearing. For this, various design approaches have been developed. The earliest technique is warped filter design, where the delay elements in traditional FIR or IIR filters are substituted by identical first-order allpasses. Kautz filters can be seen as the generalization of warped FIR filters where the allpasses can be different, leading to a complete freedom in setting the frequency resolution by the suitable choice of pole frequencies. Fixed-pole parallel filters provide the same flexibility as Kautz filters (more about the mathematical equivalence with Kautz filters in [Bank AES128]), while require only 4 multiplications and 4 additions for a second-order section, as opposed to 6 multiplications and 8 additions for the Kautz filter.

Implementing IIR filters in the form of parallel second-order sections has been used traditionally because it has better quantization noise performance and the possibility of code parallelization. The parameters of the second-order sections are usually determined from direct form IIR filters by partial fraction expansion. On the contrary, in the context of fixed-pole parallel filters (termed parallel filters in the following), the filter poles are set to a predetermined positions, leaving only the zeros as free parameters for optimization. This might seem as a limitation at first glance, but actually this allows us to gain complete control over the frequency resolution of filter design. For example, by setting the poles according to a logarithmic frequency scale, the design will have a logarithmic frequency resolution.

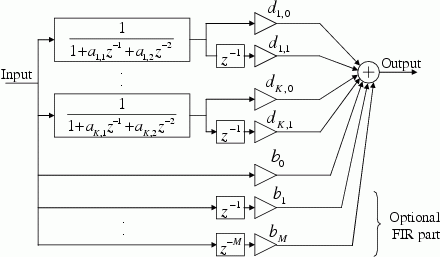
Fig. 1: the structure of the fixed-pole parallel filter.

The structure of the parallel filter is displayed in Fig. 1. The second-order sections can be augmented by an optional parallel FIR part if required (this is beneficial for modeling non-minimumphase responses [Bank ICMC07]).

2 Filter design

It can be seen in Fig. 1 that once the poles (and thus the denominator coefficients ak,1 and ak,2) are determined, the filter design problem becomes linear in its free parameters (the dk,1 and dk,2 output weights). Basically, the parallel filter models a given target impulse response as a linear combination of exponentially decaying sinusoidal functions generated by the 1/(1+ak,1+ak,2) terms. In the case of the optional FIR part, the model is extended by delayed unit pulses. As for all linear-in-parameter problems, the filter weights can be estimated by the least-squares (LS) equation and thus the coefficients are obtained in a closed form:

popt = (MH M)MH ht

where the M matrix contains the modeling signals, which are the exponentially decaying sinusoidal functions given by the denominator terms 1/(1+ak,1+ak,2) and the delayed unit pulses of the FIR part. The target impulse response is given in ht. The above equation gives the popt containing the optimal set of filter weights (d and b coefficients) in such that the filter impulse response (h=Mpopt in matrix form) is the closest to the target impulse response ht in the mean squares sense.

Now we have only considered time-domain design, when the target impulse response of the filter is specified. However, the parallel filter can also be designed in the frequency-domain, when the filter specification is available as a frequency response. Since the problem is still linear in its free parameters, the optimal set of coefficients is again obtained by a linear LS design [Bank SPL11]. Note that the time-domain and frequency-domain designs practically lead to the same filter, and that in frequency-domain design the complex frequency response is approximated, that is, the parallel filter models (or equalizes) both magnitude and phase.

Equalizing a system (such as a loudspeaker) can be done by first "inverting" the system response in the frequency-domain, and then designing a parallel filter which approximates this inverted response. However, better results are achieved if the equalizer is designed directly, without response inversion. In this case the input of the filter is the system response, and the filter weights should be adjusted so that the linear combination of the filtered signals are closest to the response we would like to achieve. This again leads to the same LS equations as discussed above (see [Bank SPL08] for time-domain and [Bank SPL11] for frequency-domain equalizer design).

As can be seen in the above discussion, estimating the weights of the parallel filter is fast and straightforward. We note again that the weights are given by a closed form formula, so it is hard to do anything wrong here. Thus, in parallel filter design the only thing we have to do right is the choice of pole frequencies, which is the topic of the next section.

3 Pole positioning

There are basically two different ways of choosing the pole frequencies, depending on the system to be modeled or equalized. In general, if the filter order is in the same range as the system order, we do have some hope to model the system precisely, thus, the filter poles should correspond to system poles for best accuracy. This is related to parametric modeling of transfer functions. On the other hand, if the system order is many orders of magnitude larger than the filter order, we can only model the average trend of the system response. In this case the pole set should be chosen based on how much resolution we wish to achieve at different frequencies. This is more like a nonparametric approach.

3.1 Pole positioning based on IIR filter design

In this case an IIR filter is designed (e.g., by the Steiglitz-McBride method) based on the target response, and the poles of this IIR filter are found as the roots of the denominator. Then these poles are used as the poles of the parallel filter. This method is advantageous when the order of the filter is in the same range as the order of the system to be modeled, since in this case the filter poles will correspond to system poles. Of course standard IIR filters have a linear frequency resolution, so for audio, we rather design a warped IIR (WIIR) filter, find the poles and dewarp them. In this case the frequency resolution is set by the warping parameter, and the parallel filter response is practically the same as of the warped filter from which its poles originate [Bank ICMC07].

For some applications the resolution profile of a single warped filter can be limited. For example, achieveing a logarithmic frequency resolution in the full audio bandwidth (from 20 Hz to 20 kHz) is not possible with a warped filter. In this case it is possible to design more warped IIR filters to the same target response using different warping parameters (in practice, usually two WIIR designs are sufficient). Then, the poles of these WIIR filters are computed, dewarped, and the pole sets are united [Bank and Ramos SPL11]. Another (bit more complicated) option is splitting the target response into subbands, and stretching these bands to the full digital frequency range (e.g., by a linear transformation in the frequency-domain, or by decimation in the time-domain), and designing the (warped) IIR filters in these subbands. Then, the poles are dewarped and transformed back to the original frequency scale, and finally the pole sets are united.

The IIR design based pole positioning method has been succesfully used for modeling the radiation behavior of the piano soundboard [Bank ICMC07], and for the modeling of guitar admittance responses [Bank and Karjalainen Acoustics08, Bank and Karjalainen DAFx10].

3.2 Predetermined pole set based on the required resolution

If the system order is significantly larger compared to the filter order, the previous technique based on IIR filter design will not work because the IIR design algorithm will pick and model a few resonant peaks while the others are not modeled. Therefore, the filter will not follow the overall system response. In this case, better results are achieved if the pole frequencies are set to a predetermined frequency series, and the pole radii are set in a way that the frequency responses of the second-order sections cross at their -3dB points. It can be shown that in this case the filter response will be the complex-smoothed version of the target response, and the width of the smoothing window actually equals the pole frequency distance in that frequency region [Bank AES128]. For example, for achieving a 6th octave resolution, we have to place 3 pole frequencies in each octave on a logarithmic frequency grid. Of course the resolution does not have to be logarithmic, it is also possible to use different pole frequency distances in the different regions.

This way of pole positioning is particularly usefull for the equalization of loudspeaker-room responses, due to the high order of the system to be equalized. In addition, for equalization the smoothing of the loudspeaker-room response would be necessary anyway to avoid the typical problems of direct inversion (like compensating the deep notches by large peaks), and this smoothing is done automatically by the parallel filter design with a predetermined pole set. Another great advantage is that the design is very much simplified since all we have to do is to set the poles and then calculate the weights by the LS design (there is no need for prior IIR filter design as with the previous approach). More details about this kind of pole positioning and its automatic smoothing effect are in [Bank AES128].

3.3 Pole positioning based on smoothed responses

While the predetermined (e.g. logarithmic) pole set works very well for high order systems, it is still possible to increase the filter design accuracy at a given filter order, at the price of increased design complexity. This is because some regions of the system response are more "smooth" than others, and a strictly logarithmic frequency resolution may waste some computational resources at these already smooth regions. For example, a typical loudspeaker-room response has much larger ripples at low frequencies compared to the high ones. This can be taken into account in a simple way by setting higher pole density for low frequencies manually, as was done in the design example of [Bank SPL08]. However, this requires some user interaction. It would be more desirable to have such a method that automatically recognizes which regions need higher resolution.

The basic idea is that the target response is smoothed to the required resolution (which again can be different in the various frequency regions), and then this smoothed response is used to determine the optimal pole set of the filter. A straightforward and nicely working solution is to design a warped IIR filter to the smoothed response, obtain the poles and dewarp them. If the modeling or equalization have to be done in a wider frequency range, it is again beneficial to design more warped IIR filters to the same response with different warping parameters, and unite the poles [Bank and Ramos SPL11]. Basically, the same procedures can be applied as was presented in Sec. 3.1 about IIR filter based pole positioning, but now the target response is smoothed before filter design. This will in general give a better fit compared to the predetermined pole set of Sec. 3.2, but the design becomes more complex by the additional transfer function smoothing and warped IIR filter design. This technique has been applied to loudspeaker-room response equalization in [Bank and Ramos SPL11], providing superior performance compared to various earlier filter design methods.

A nice compromise between simplicity of design and accuracy is automatically placing the poles depending on the ripple density of the transfer function. This technique is described in [Bank AES51], together with a comparison of all the different pole positioning techniques, including warping, multi-band warping and custom warping.

3.4 Combined approaches

Of course it is possible to use the combination of the above mentioned approaches, that is, using different methods in different frequency bands. For example, for modeling a guitar admittance it would make sense to use a precise model for low frequencies, where the modal density is low (we have good chances for an accurate model). Therefore, at low frequencies, the poles are estimated by a (warped) IIR filter according to Sec. 3.1, while in the region of modal overlap, the poles are set to a logarithmic frequency resolution as in Sec. 3.2. The same ideas could be used for loudspeaker-room response equalization, again because at low frequencies the room modes are distinct, while above the Schroeder frequency they cannot be discriminated because of the high modal overlap. A similar effect can be achieved by combining the methods of Secs. 3.1 and 3.3 if we simply do not apply smoothing in the low modal density range, but we do smooth the response above, and design the WIIR filter (or filters) to this partially smoothed response.

4 Design examples

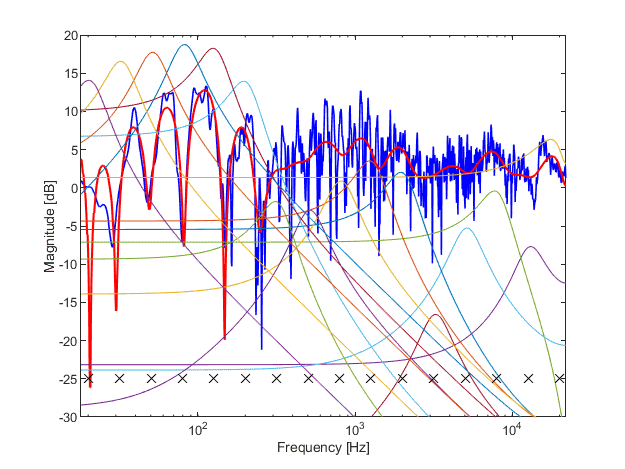
In the following, a simple parallel filter design example is shown based on predetermined (logarithmic) pole positioning with third octave resolution. For this, 16 pole pairs are inserted from 20 Hz to 20 kHz on a logarithmic grid, indicated by green lines in Fig. 2. The target is a loudspeaker-room response (blue line), and it can be seen that the filter response (red line) follows the local average of the target (it looks like the smoothed version of the blue curve).

Fig. 2: Parallel filter design example. Blue: filter specification (loudspeaker-room response), red: resulting filter frequency response, thin colored lines: the individual transfer functions of the 16 second-order sections. The black crosses display the pole frequencies.

In addition, the individual transfer functions of the 16 second-order sections are also displayed, to give an intuition how the final response arises as the combination of the individual responses. It can be seen that the final transfer function is a result of a complicated interaction of the basis functions, unlike in a graphic equalizer. This is because now not only the gains but also the phases of the different "bands" are free parameters. As an effect, while the width of the resulting peaks is limited by the Q factors of the sections, the dips can be much narrower, since they arise from phase cancellations of neighboring bands. You can generate a similar figure by placing the poles at wish by a click of a mouse: just run the parfiltdemo script from the MATLAB code section.

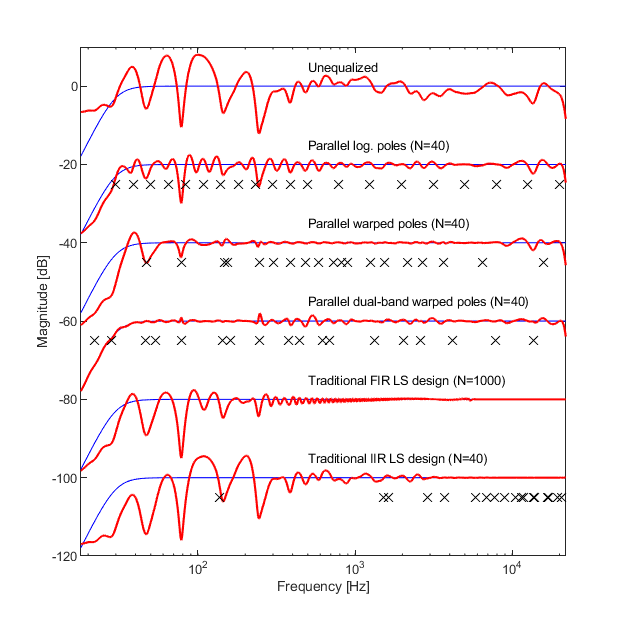
The next figure displays a room equalization example using a 40th order parallel filter. The first curve is the original (unequalized) response of the loudspeaker smoothed to sixth-octave resolution, next is the one equalized by stepwise logarithmic pole positioning having higher pole density, thus higher resolution at low frequencies. This is followed by a warping based design using a single lambda of 0.9. It can be seen that while this provides accurate results in the mid frequency range, it cannot equalize the response at the edges of the full frequency band. This is resolved by splitting the frequancy range and using two different lambda parameters for low and high frequencies (0.986 and 0.65) in dual-band warping, providing excellent equalization in the fulll audio frequency range.

On the contrary, traditional least squares FIR design shown by the penultimate curve in Fig. 3 is unable to provide an acceptable low-frequency equalization even at a high filter order of N=1000 due to its inherently linear frequency resolution. Similar results are obtained using traditional IIR filter design, displayed by the last curve. Note that even the simplest form of fixed-pole parallel filter design using logarithmic pole frequencies (second curve) significantly outperforms the traditional IIR filter of the same order.

Fig. 3: Equalizing a smoothed loudspeaker-room response with parallel filters: three different pole positioning methods and a comparison to traditional filter design. Filter order is N=40, except for the FIR filter, where N=1000. Blue: target response, red: equalized response, crosses: pole frequencies. The curves are offset for clarity.

5 Extensions and applications

5.1 Multichannel crosstalk-cancellation using parallel filters

While it is well known that IIR filters require lower filter order for a given accuracy compared to FIR filters, the extension if IIR filter design techniques to the multichannel case is far from trivial. Due to this reason in multiple-input multiple-output (MIMO) equalization almost always FIR filters are applied. However, by noting that the fixed-pole design of parallel filters is mathematically very similar to a FIR design due to its linear-in-parameter form, it turns out that parallel filters can be applied to MIMO problems just as simply as FIR filters. On the other hand, the flexibility in allocating the frequency resolution leads to significant computational savings. In [Bank JAES18] the method is applied to the crosstalk-cancellation of a spherical loudspeaker array and shown that for this example only 1/4 of arithmetic operations are required compared to FIR filters for the same crosstalk.

5.2 The delayed parallel filter

In the parallel filter structure (Fig. 1), there is an optional FIR part that is beneficial for efficient modeling and equalization of non-minimumphase responses. In the original configuration, the FIR and IIR parts overlap in time. In practical implementations using finite wordlength, due to this overlap the gain of the sections and that of the FIR filter can be significantly higher than that of the final transfer function, which requires the downscaling of the filter coefficients to avoid overflow. This leads to a significant loss of useful bitdeph, which can be problematic in practical implementations. The solution is delaying the IIR part so that there is no overlap between the responses of the FIR part and the second-order sections [Bank and Smith AES136]. Matlab code for obtaining a delayed parallel filter from the non-delayed one (and from direct form B(z)/A(z) transfer functions) can be found at http://www.mit.bme.hu/~bank/delparf.

5.3 Converting direct- or series-form IIR filters to parallel form

Traditionally, parallel second-order sections are used because their better numerical properties compared to direct-form IIR filters and their coefficients are obtained by partial fraction expansion from the direct-form IIR filter. It turns out that by doing so the same dynamic range problem arises as described in 5.1 if the numerator order is larger or equal than the order of the denominator. This is demonstrated in [Bank SPM18]. In addition, the usual conversion of partial fraction expansion cannot be performed for high (N>200) filter orders due to the numerical sensitivity in pole finding. Therefore, the same paper provides a robust conversion method that can be used for very high (N~1000) filter orders. Matlab code for converting direct form and series second-order form IIR filters to parallel filters can be downloaded from "http://www.mit.bme.hu/~bank/parconv".

5.4 Magnitude-priority filter design

A notable side-effect of quasi-logarithmic frequency design methods (thus, also the parallel filter) is a high-frequency attenuation for non-minimumphase targets. This is because filter design acts similarly to frequency-dependent windowing with shorter window length at high frequencies [Bank AES128]. When the target is made minimum-phase prior to filter design, energy becomes concentrated in the early part of the response, avoiding the problems of this windowing behavior. However, this results in magnitude-only filter design, and means the phase information is lost (unless the system is minimum-phase anyway, as for a mechanical admittance, for example).

The magnitude-priority method described in [Bank AES132] combines the complex and magnitude-only approaches in such a way that the filter follows both magnitude and phase in those frequency regions where it can, while where this is not possible, it focuses on the magnitude. The method can be implemented either by the iterative update of the magnitude, or by the iterative update of the phase of the target specification. While in [Bank AES132] these two variants are demonstrated by parallel filter designs, they are equally applicable to other techniques, like standard FIR, IIR, warped FIR, warped IIR, or Kautz filters.

5.5 Nonlinear modeling with fixed-pole parallel filters

Many audio systems show some form of nonlinear behavior that has to be taken into account in modeling. For this, often a black-box model is identified, coming from the generality and simplicity of the approach. Parallel filters can be efficiently utilized in polynomial Hammerstein models that use parallel branches with a polynomial-type nonlinearity and a linear filter in series. The efficiency comes from the MISO (multiple input singe output) structure of the polynomial Hammerstein model, which allows the use of common denominator parts for the parallel filter, practically halving the required computational complexity. Due to its efficiency, the approach is particularly well suited for the real-time digital simulation of weakly nonlinear devices, such as loudspeakers, headphones, or tube guitar amplifiers [Bank AES130, Romoli et al. AES136].

5.6 The passive parallel filter

The fixed-pole parallel filter can also be used for modeling passive (positive real) transfer functions. In physics-based sound synthesis, when modeling a mechanical admittance (like the admittance of a guitar bridge), the amittance filter transfer function must be passive, in order to guarantee the stability of the model. In this case, a special form of parallel filter is designed by constrained LS optimization that fits a passive filter to the measured transfer function, even if the original transfer function is not passive due to measurement errors. More details for the 1D and multi-dimensional (MIMO) case can be found in [Bank and Karjalainen Acoustics08] and [Bank and Karjalainen DAFx10], respectively.


Video tutorial

CLICK HERE FOR THE VIDEO TUTORIAL (mp4 file), Slides in pdf

Balázs Bank, "Perceptually motivated filter design with applications to loudspeaker and room equalization," Tutorial presented at Virtual Vienna AES Convention on 2nd of June, 2020. 		This tutorial gives a 40 minutes summary about filter and equalizer design for audio with an emphasis on parallel filters and provides quite a few examples on loudspeaker-room response equalization.

Related publications

Tutorial paper + book

[Bank JAES22] - Balázs Bank, "Warped, Kautz, and Fixed-Pole Parallel Filters: A Review", The Journal of the Audio Engineering Society, Vol. 70, Iss. 6, pp. 414-434. June 2022 A tutorial about logarithmic frequency resolution filter design: a good starting point about warped, Kautz and parallel filters. Summazrizes the main results of my earlier publications
[Bank MTA21] - Balázs Bank, Logarithmic frequency resolution filter design for audio applications, Doctor of the Hung. Acad. of Sci. thesis, Hungarian Academy of Sciences (MTA), Hungary, p. 120, July 2021. A 100 page (+ appendix) book mostly about fixed-pole parallel filters but discusses quite a lot about warped and Kautz filters as well. In a way an extended version of the above [Bank JAES22] in a form of a thesis book.

Standard parallel filter design

[Bank SPL08] - Balázs Bank, "Perceptually Motivated Audio Equalization Using Fixed-Pole Parallel Second-Order Filters,'' IEEE Signal Processing Letters, Vol. 15, pp. 477-480, 2008. Abstract and Matlab code A concise (four pages) description of parallel filter design with the application to loudspeaker-room response equalization. Comparison to IIR, WFIR, WIIR and Kautz filters. Start with this one.
[Bank AES51] - Balázs Bank, "Loudspeaker and room response equalization using parallel filters: comparison of pole positioning strategies," Proceedings of the 51st AES Conference, Helsinki, Finland, August 2013. A comparison of different pole positioning strategies: a nice overview. This would be the second paper to check out.
[Bank AES128] - Balázs Bank, "Audio Equalization with Fixed-Pole Parallel Filters: An Efficient Alternative to Complex Smoothing," 128th AES Convention, Preprint No. 7965, London, UK, May 2010. (The journal version of this paper is available at AES E-library) This paper discusses the automatic smoothing behavior of the parallel filter design and relates parallel filters to Kautz filters.
[Bank SPL11] - Balázs Bank, "Logarithmic Frequency Scale Parallel Filter Design with Complex and Magnitude-Only Specifications," IEEE Signal Processing Letters, Vol. 18, No. 2, pp. 138-141, Feb. 2011. This paper is about the frequency-domain design of parallel filters, including a magnitude-only variant, and the use of frequency-dependent weighting.
[Bank and Ramos SPL11] - Balázs Bank and Germán Ramos, "Improved Pole Positioning for Parallel Filters Based on Spectral Smoothing and Multiband Warping," IEEE Signal Processing Letters, vol. 18, no. 5, pp. 299-302, Mar. 2011. This paper is about a pole positioning method for the parallel filter which designs multiple warped IIR filters for the various parts of the smoothed target resposne and uses the united pole set of the warped designs.
[Bank ICMC07] - Balázs Bank, "Direct Design of Parallel Second-Order Filters for Instrument Body Modeling", Proceedings of the International Computer Music Conference (ICMC07), vol. I., pp. 458-465, Copenhagen, Denmark, Aug. 2007. Abstract, Matlab code and sound examples This paper applies the parallel filter to piano soundboard radiation modeling. It presents logarithmic and warped IIR based pole positioning examples and non-minimumphase modeling by utilizing the optional FIR part. It also presents comparisons to IIR filters at various filter orders.
[Bank JAES18] - Balázs Bank, "Multichannel Equalization and Crosstalk Cancellation Using Fixed-Pole IIR Filters", (Available at AES E-library) The Journal of the Audio Engineering Society, Vol. 66, Iss. 11, pp. 901-909, Nov. 2018. Here the MIMO extension of parallel filter design is developed and demonstrated by the crosstalk-cancellation of a 20 element spherical loudspeaker array.

The delayed parallel filter

[Bank and Smith AES136] - Balázs Bank and Julius O. Smith, III, "A delayed parallel filter structure with an FIR part having improved numerical properties", 136th AES Convention, Preprint No. 9084, Berlin, April 2014. Abstract and Matlab/Octave code

 This paper presents an alternative form of the parallel filter where the response of the second-order IIR sections is delayed so there is no overlap with the FIR part. This leads to improved numerical performance for filters having a long FIR part. In addition, it also discusses the conversion of direct form B(z)/A(z) transfer functions to a parallel form.
[Bank SPM18] - Balázs Bank, "Converting Infinite Impulse Response Filters to Parallel Form", (Also available at IEEEXplore) IEEE Signal Processing Magazine, Vol. 35, Iss. 3, pp. 124-130, May 2018. Abstract and Matlab/Octave code

This paper demonstrates that the numerical problem of the original, non-delayed parallel structure exists also when the common practice of converting from direct-form IIR filters is applied, and shows how this can be avoided using the delayed parallel form. In addition, it provides a numerically more robust conversion method compared to the usual partial fraction expansion, allowing the conversion of filters having very high (N~1000) order.

Magnitude-priority filter design

[Bank AES132] - Balázs Bank, "Magnitude-Priority Filter Design for Audio Applications,"132nd AES Convention, Preprint No. 8591, Budapest, Hungary, April 2012. In magnitude-priority filter design the idea is modeling both magnitude and phase in those frequency regions of the target where this is possible, while where this is cannot be achieved due to low filter order, the method prioritizes magnitude accuracy. The method is demonstrated using parallel filter designs.

Nonlinear modeling with the parallel filter

[Bank AES130] - Balázs Bank, "Computationally efficient nonlinear Chebyshev models using fixed-pole parallel filters with the application to loudspeaker modeling,"130th AES Convention, Preprint No. 8426, London, UK, May 2011. This paper is about the efficient implementation of polynomial Hammerstein models using common-denominator parallel filters. For the nonlinearity, Chebyshev polynomials are used, allowing the identification of the linear transfer functions by the logarithmic sweep method.
[Romoli et al. AES136] - Laura Romoli, Stefania Cecchi, Balázs Bank, Michele Gasparini, and Francesco Piazza, "Application of common-pole parallel filters to nonlinear models based on orthogonal functions", 136th AES Convention, Preprint No. 9068, Berlin, April 2014. This paper is the extension of [Bank AES130], where both Chebyshev and Legendre polynomials are tested, and the identification is done using a frequency-domain adaptive filter with a white noise input. Comparison with an FIR filter based model is also given.

The passive parallel filter

[Bank and Karjalainen Acoustics08] - Balázs Bank and Matti Karjalainen, "Passive Admittance Synthesis for Sound Synthesis Applications," Proceedings of the Acoustics'08 Paris International Conference, paper id: ACOUSTICS2008/254, Paris, France, June 2008. This paper is about modeling a 1D passive admittance (point mobility) by a parallel filter designed with warped pole positioning and nonnegative LS optimization. The admittance is then converted to a reflectance filter and used in a digital-waveguide guitar model.
[Bank and Karjalainen DAFx10] - Balázs Bank and Matti Karjalainen, "Passive Admittance Matrix Modeling for Guitar Synthesis," Proceedings of the 13th International Conference on Digital Audio Effects (DAFx-10), pp. 3-7, Graz, Austria, Sept. 2010. Abstract and sound examples This paper is the multidimensional extension of [Bank and Karjalainen Acoutics08] with warped common-pole pole positioning. The admittance matrix is again converted to a reflectance matrix and connected to a dual polarization digital waveguide string model.

You may check my entire list of publications.


MATLAB/Octave code

Here you can find some MATLAB functions for designing parallel second-order filters, which should also work in Octave:

And here are some Matlab example files that can help in understanding how to use the above functions (all files as a zip file):

(c) Balazs Bank, 2024. All rights on the content of this site (including the description, video, pdf files and Matlab/Octave codes) reserved to the author. Non-commercial use permitted, for all other uses, please contact the author.

Home Page E-mail to Me
Last modified: 24.03.2024.